Simulations and models
In this chapter we will create a simulation of the behaviour of many interacting objects. A class describing
the behavior and properties of these objects will be defined. We will show how to control them with the use of
a timer and signals, and how to pass variable values between the objects.
This chapter is dedicated to intermediate-level users. Before reading, it is advisable to look into
the handbook, into the chapter on POOL classes.
1. The first model.
 At the beginning, we will write a very simple class, to be developed in following chapters.
At the beginning, we will write a very simple class, to be developed in following chapters.
A class in POOL is defined exactly in the same way as a function. In fact, a new object (a turtle) performs at
the creation stage the function that defines its class. All the functions and variables then created become the
members of that object. Also the parameters of the creating function are preserved for the object’s lifetime as
local variables.
In the first version of the program, a model class allows for setting simple features of a turtle:
its initial position, heading and speed. These values are passed as arguments of the function that creates the
turtle - let’s call this function the constructor. The constructor sets also a drawing colour and a
radius of the turtle (now used at bouncing off a wall). Finally, the constructor outputs information on the
turtle’s new parameters in a text window.
A model class has one member function: step dt.
This function allows to move a turtle forward by a distance resulting from its speed
(given as the constructor’s argument) and the dt period of time given as an argument of
the function.
The main turtle (#first) program creates two model class turtles. The description of
the newturtle command used to do this can be found in the handbook.
To move the turtles, the repeat loop calls the step function for each of them. The
function to be performed by objects is called by the @ operator in POOL.
A delay in a loop allows to keep a constant pace of program operation execution, appropriate for turtle speed
settings.
to model :p :h [:v 60]
setpos :p
setheading :h
setpencolor random 1000
pendown
showturtle
setradius 10
to step :dt
right (runif -20 20)
forward 0.001 * :dt * :v
end
(print who "|p =| :p "|h =| :h "|v =| :v)
end
bounce
hideturtle penup
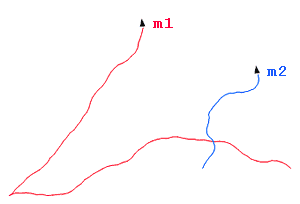
"m1 := (newturtle $model {-50 0} 30 15)
"m2 := (newturtle $model {50 0} (-50))
"dt := 100
repeat 500 [
sync :dt
(step :dt) @ :m1
(step :dt) @ :m2
]
2. More independence.
 In the previous chapter, the
In the previous chapter, the #first turtle controlled the :m1 and :m2
turtles, by issuing commands for them in a loop. A better way of regular command calling is to do it with a
timer. A timer does not require programming of delays (sync or wait) and does not
block the access to the #first turtle in the command line. In the next version of the program we
will use a timer.
The handbook explains how to use a timer. Now, we will use a version, where a
timer sends a signal to all the turtles at regular intervals. In the class describing our model, we can receive
such a signal with an appropriate handling function - such function will replace the step function
from the previous chapter. A value of time needed to calculate the length of the turtle step can be taken from
the information included in the signal sent by the timer.
At this stage, we also change the method a new turtle is created. An event handling function is added to the
#first turtle program - it handles clicking a mouse (see the description in the handbook).
At each click, a new turtle will now appear in the graphic window, and it will immediately begin to handle
the signals sent by the timer.
After starting the program and creating a few turtles, switch into the command line. You can give commands -
the #first turtle is busy with executing the timer function for a mere fraction of a millisecond.
You can check e.g. how many turtles have been created so far: print count children.
to model :p :h [:v 60]
setpos :p
setheading :h
(setpencolor random 1000 75)
pendown
showturtle
setradius 10
to onsignalstep :turtle :data
right (runif -20 20)
let "dt :data,2
forward 0.001 * :dt * :v
end
(print who "|p =| :p "|h =| :h "|v =| :v)
end
to onmouseclick :mousepos
let "m (newt $model :mousepos random 360 20 + random 100)
end
bounce ht pu
"t := timer "step 500
3. More cooperation.
 In previous programs, each turtle followed its own track and there was no interaction between them. In this chapter, we will make them communicate. Instead of executing random turns, we will calculate a new direction of a turtle in each step
- slightly towards other turtles.
In previous programs, each turtle followed its own track and there was no interaction between them. In this chapter, we will make them communicate. Instead of executing random turns, we will calculate a new direction of a turtle in each step
- slightly towards other turtles.
The onsignalkrokstep handling function is changed - instead of the right (runif -20 20)
turn, we will use a command that will position a turtle according to a given vector: setheaddir turn;
turn is a new member function of the model class. It includes a several new elements:
all - a command returning the list of all the turtles existing in the program;
this - a command returning the turtle which called the command; in this case, it allows to avoid calculating the
"towards itself" direction: :m <> this;
pos @ :m - reading the position of other turtles.
to model :p :h [:v 60]
setpos :p
setheading :h
(setpencolor random 1000 75)
pendown
showturtle
setradius 10
to turn
if (count all) > 2 [
let "sx 0 let "sy 0
foreach "m all [
if and (:m <> this) (:m <> #first) [
let "pm pos @ :m
let "dx :pm,1 - xcor
let "dy :pm,2 - ycor
let "norm sqrt :dx^2 + :dy^2
"sx := :sx + :dx / :norm
"sy := :sy + :dy / :norm
]
]
"sx := 0.1 * :sx + 0.9 * headdir,1
"sy := 0.1 * :sy + 0.9 * headdir,2
output array :sx :sy
]
output headdir
end
to onsignalstep :turtle :data
setheaddir turn
fd 0.001 * :data,2 * :v
end
(print who "|p =| :p "|h =| :h "|v =| :v)
end
to onmouseclick :mousepos
let "m (newt $model :mousepos random 360 50 + random 100)
end
bounce ht pu
setpalette "hot
"t := timer "step 50
 The program above looks reasonably and it operates according to our expectations. However, to prepare a more interesting and complex simulation, we need a stricter order
- a division into two stages:
The program above looks reasonably and it operates according to our expectations. However, to prepare a more interesting and complex simulation, we need a stricter order
- a division into two stages:
calculating changes - preparation of new values for direction, speed, etc.; the state of all the objects is
"frozen" and the objects can read each other’s state;
applying changes - the state of objects changes according to the values calculated at the preceding stage; the objects do not communicate with each other.
Such a division allows for simultaneous calculations at each stage, and yields the results that are
independent of the calculation running sequence. In order to realize this algorithm, the operation of
the timer has to be adjusted so that at each "tick" it would send two signals: the "turn" signal, on
which the handling function in the model class will calculate new direction of the turtle
on the basis of the arrangement of other turtles; and the "step" signal which will make each turtle
turn and move a step ahead. The signals in the new program of the timer are "blocking" signals
(see the description in the handbook), that is: execution of commands
by the program that has sent a signal is stopped until all the objects finish to handle the signal
that has been sent.
Another improvement of the new version is the feature that allows for storing the model class turtles
in a shared variable (one copy of a variable is available for all the objects): shared "turtles.
Thus, searching the turtle list while a new direction is being calculated is a bit easier.
shared "turtles
"turtles := []
to model :p :h [:v 60]
setpos :p
setheading :h
(setpencolor random 1000 75)
pendown
showturtle
setradius 10
let "dir headdir
to onsignalturn
if (count :turtles) < 2 [
"dir := headdir stop
]
let "sx 0 let "sy 0
foreach "m :turtles [
if :m <> this [
let "pm pos @ :m
let "dx :pm,1 - xcor
let "dy :pm,2 - ycor
let "norm sqrt :dx^2 + :dy^2
"sx := :sx + :dx / :norm
"sy := :sy + :dy / :norm
]
]
"sx := 0.1 * :sx + 0.9 * headdir,1
"sy := 0.1 * :sy + 0.9 * headdir,2
"dir := array :sx :sy
end
to onsignalstep :turtle :data
setheaddir :dir
fd 0.001 * :data * :v
end
(print who "|p =| :p "|h =| :h "|v =| :v)
end
to onmouseclick :mousepos
queue :turtles (newt $model :mousepos random 360 50 + random 100)
end
bounce ht pu
setpalette "blue2red
"t := timer [
signalw "turn
(signalw "step :dt)
] 50
4. Full simulation.
We have now all the elements needed for programming a simulation. It will be a particle model with a
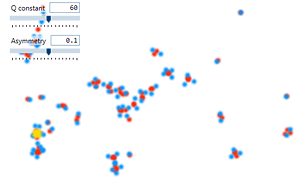
mass–dependent inertia and an attracting or repealing electric-like charge. Using GUI sliders, you can
change an interaction force (the "force" slider) and mass proportions (the "asymmetry" slider).
shared "particles
"particles := []
to model :q :mass [:v 0] [:h 0] [:ft 0.001] [:c 90]
to set_force :g
"c := -(:q * :g)
end
to set_mass :m
setr 10 * sqrt :m
"mass := :m
end
"charge := :q
set_mass :mass
set_force :c
setpos pos @ parent
seth :h
st
let "fx 0
let "fy 0
to onsignalf
"fx := 0 "fy := 0
foreach "m :particles [
if :m <> this [
let "p pos @ :m
let "r radius + radius @ :m
let "d distance :p
ifelse :d > :r
[let "fm (:c * :charge @ :m) / :d^3]
[let "fm (:c * :charge @ :m) / :r^3]
"fx += :fm * (:p,1 - xcor)
"fy += :fm * (:p,2 - ycor)
]
]
end
to onsignalstep :turtle :data
let "dt 0.01 * :data
if :dt > 0.8 ["dt := 0.8]
let "hdir headdir
:hdir,1 := :v * :hdir,1 + :fx * :dt / :mass
:hdir,2 := :v * :hdir,2 + :fy * :dt / :mass
"v := sqrt :hdir,1^2 + :hdir,2^2
if :v > 30 ["v := 30]
setheaddir :hdir
let "ds :v * :dt
"v -= :ds * :ft / :mass
if :v < 0 ["v := 0]
fd :ds
end
end
bounce ht pu
repeat 30 [
setxy (rnorm -30 30) (rnorm -10 30)
"m := (newt $model 1 0.7)
(setturtleimg "red_light_small) @ :m
queue :particles :m
]
repeat 30 [
setxy (rnorm 30 30) (rnorm -10 30)
"m := (newt $model (-1) 0.3)
(setturtleimg "blue_light_small) @ :m
queue :particles :m
]
home
"m := (newt $model 3 2 4 45 0)
(setturtleimg "yellow_light) @ :m
queue :particles :m
"gs := (slider "force {10 4} {10 100 5} 90)
setonchange :gs [
foreach "m :particles [(set_force getvalue :gs) @ :m]
]
"sym := (slider "asymmetry {10 60} {-0.9 0.9 0.1} 0.4)
setonchange :sym [
let "s 0.5 * (1 + getvalue :sym)
foreach "m :particles [
if :charge @ :m = 1 [(set_mass :s) @ :m]
if :charge @ :m = -1 [(set_mass 1 - :s) @ :m]
]
]
"t := timer [
signalw "f
(signalw "step :dt)
] 25
5. Summary.
This article presents the most fundamental techniques used for preparing a simulation consisting of many
interacting objects: the description of the properties and behavior of objects by classes, the application of
a timer for simulation steps to be taken at regular intervals, and signals - to trigger off parallel tasks.
The simulation we prepared is based on very simple principles - inertia and a force resembling an electrostatic
force. Even such a simple description allows to notice an interesting behavior of a group of objects. The
program can serve as a basis for creating a more realistic description, e.g. complemented with other ways of
interaction or with different object models. Interactive elements responding to user’s actions are also worth
adding.