Parallel Object Oriented LOGO

Funkcja rekurencyjna to taka funkcja, która zawiera wywołanie samej siebie. Użycie funkcji rekurencyjnej pozwala zapisać wiele algorytmów w czytelnej i często bardzo prostej formie. W tym rozdziale przedstawimy typowe cechy funkcji rekurencyjnych oraz jak taką funkcję zaprogramować w POOL.

Obliczanie silni

Silnia liczby naturalnej n to iloczyn wszytkich liczb naturalnych nie większych niż n: n! = 1 * 2 * 3 * ... * n. Na przykład: 5! = 1 * 2 * 3 * 4 * 5 = 120. Rekurencyjny algorytm silni można zapisać jako:

Zauważ: każdy algorytm rekurencyjny potrzebuje warunku zakończenia działania. Algorytm w punkcie a) oblicza silnię jako iloczyn liczby i silni tej liczby pomniejszonej o 1. Ten ciąg obliczeń kończy się gdy bieżąca wartość n osiągnie 1 i zostanie spełniony warunek z punktu b).

to silnia :n
  print :n                  ;wypisz bieżącą wartość n
  if :n <= 1 [output 1]     ;warunek zakończenia obliczeń
  output :n * silnia :n - 1 ;obliczenie n * (n-1)!
end

(print "wynik silnia 5)

Funkcja silnia posiada jeden argument: liczbę n, a jako wynik zwraca wartość n!. Sposób zdefiniowania takiej funkcji opisaliśmy już w poprzednim rozdziale. Tu pojawia się po raz pierwszy instrukcja warunkowa: if. Pozwala ona wykonać blok kodu umieszczony w liście (tu: output 1) tylko jeśli spełniony jest warunek podany w pierwszym argumencie instrukcji (tu: :n <= 1).

Dla zilustrowania kolejności obliczeń funkcja silnia w każdym wywołaniu wypisuje wartość argumentu :n. Zauważ, że pojedyńcze wywołanie silnia 5 powoduje wypisanie liczb od 5 do 1. Dzieje się tak dlatego, że funkcja wywołuje samą siebie dla kolejnych wartości aż do 1. Wiąże się z tym ważna cecha funkcji rekurencyjnych : w czasie wykonania funkcji w pamięci przechowywane są argumenty i zmienne lokalne wszystkich rekurencyjnych wywołań funkcji. Ilość pamięci potrzebna do wykonania funkcji rekurencyjnej może być istotnym czynnikiem podczas programowania algorytmu. Należy wtedy pomyśleć nad standardowym, nierekurencyjnym odpowiednikiem. W przypadku silni może to być np. taka funkcja:

to silnia_1 :n
  if :n <= 1 [output 1] ;zwróć 1 dla 0! i 1!
  let "k :n             ;utwórz zmienną lokalną k = n
  while :n > 2 [        ;powtarzaj dopóki n > 2
    "n := :n - 1        ;pomniejsz n o 1
    "k := :k * :n       ;oblicz kolejny iloczyn
  ]
  output :k             ;końcowy wynik: k = n!
end

Ta funkcja używa dwóch zmiennych: argumentu :n i zmienej lokalnej :k do obliczenia silni z dowolnej wartości.

Proste fraktale

Używając funkcji rekurencyjnych łatwo można zaprogramować rysowanie fraktali - figur, których mniejsze fragmenty są podobne do większych części lub całej figury. Poniżej przedstawiamy dwa przykłady wybrane z projektu fraktale cz.I.

Płatek Kocha

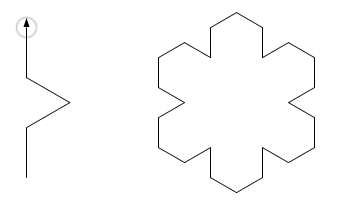
Pojedyńcze wywołanie k1 rysuje bok figury o rozmiarze :r, jak na rysunku po lewej. Sześciokrotne powtórzenie z obrotem dopełnia figurę, jak na rysunku po prawej.

Teraz prosta zmiana: każdy krok fd :r/3 zamieniamy na rekurencyjne wywołanie koch :r/3 :g-1, w którym jednocześnie zmniejszamy licznik wywołań :g; warunkiem przerwania rekurencji jest :g = 0:

to koch :r :g
  if :g = 0 [fd :r stop]
  koch :r/3 :g-1 rt 60
  koch :r/3 :g-1 lt 120
  koch :r/3 :g-1 rt 60
  koch :r/3 :g-1
end

repeat 6 [koch 90 5 rt 60]

Drzewo

Drzewo to inny popularny rodzaj fraktala. Modyfikując poniższy program można otrzymać różne formy. Także liście paproci umieszczone w projekcie należą do tej kategorii rysunków.

to drzewo :r :g
  if :g > 0 [
    setpensize :g ;grubość linii maleje z licznikiem rekurencji
    fd :r
    lt 20
    drzewo :r * 0.7 :g - 2 ;krótsza lewa gałąź
    rt 40
    drzewo :r * 0.9 :g - 1 ;dłuższa prawa gałąź
    lt 20
    pu bk :r pd
  ]
end

drzewo 100 15

Rekurencja wzajemna

Dwie niezależne funkcje mogą wywoływać się nawzajem, jak w poniższym przykładzie krzywej Wirth'a:

to wi :n :a :h :k
  if :n = 0 [fd :h stop]
  rt :a iw :n (-:a) :h :k lt :a fd :h
  lt :a iw :n (-:a) :h :k rt :a
end

to iw :n :a :h :k
  rt :a wi :n - 1 (-:a) :h :k fd :k lt 2 * :a
  fd :k wi :n - 1 (-:a) :h :k rt :a
end

to wirth :n :s
  repeat 4 [
    wi :n 45 3*:s :s
    fd :s rt 90 fd :s
  ]
end

ht wirth 4 2

Rekurencja tego rodzaju zawsze może zostać zamieniona na pojedynczą funkcję rekurencyją wi przez zastąpienie wywołań iw kodem tej funkcji, choć otrzymany w ten sposób kod może być mniej przejrzysty.
Wzajemna rekurencja jest stosowana w praktyce w parserach stosujących rekurencyjnie analizę zstępującą składni.

Ciąg Fibonacciego

Często przytaczanym podstawowym przykładem zastosowania rekurencji jest obliczanie kolejnych elementów ciągu Fibonacciego. Liczby w tym ciągu to f₀ = 0, f₁ = 1, f_n = f_n-1 + f_n-2.
Rekurencyjna funkcja może wyglądać następująco:

to fibo_rec :n
if :n < 2 [output :n]
output (fibo_rec :n-2) + (fibo_rec :n-1)
end

Choć funkcja jest bardzo prosta, to już dla elemtów ciągu o numerze 30-40 czas obliczeń rekurencyjnych jest zauważalny... dzieje się tak dlatego, że jedno wywołanie funkcji w programie powoduje dwa wyołania rekurencyjne, które z kolei wywołują po dwa razy funkcję itd, aż do sumarycznej liczby wywołań 331160281 dla n = 40. W tym przypadku algorytmiczny odpowiednik rekurencji jest bardzo pomocny, spróbuj poniższej funkcji:

to fibo_alg :n
  if :n < 2 [output :n]
  let "n2 0
  let "n1 1
  let "nx 0
  repeat :n-1 [
    "nx := :n2 + :n1
    "n2 := :n1
    "n1 := :nx
  ]
  output :nx
end

Dla ciągu Fibonacciego, jak dla każdego ciągu, w którym elementy są określone przez liniową kombinację wcześniejszych elementów ze stałymi współczynnikami, można podać wzór na n-ty element. Ten sposób obliczeń jest ostatecznie najbardziej wydajny:

Istnieje także uogólniona wersja ciągu Fibonacciego dla liczb zespolonych. Można go przedstawić na płaszczyźnie liczb zespolonych kolorując punkty według algorytmu escape time, używanego często w rysowaniu fraktali - wynikiem są obrazy jak ten przedstawiony poniżej (również wykonany w POOL). Jednak temat ten zostawiamy na osobny artykuł.